1. はじめに
エスチャリー(河口域)は陸域からの淡水と外海からの海水とが混在する水域である.その密度の不均一から密度流を生じ,かつ地形の変化も大きいため複雑な循環形態を形成している.また,エスチャリーはその特性から生産活動も活発である一方,自然外力も大きくそれらの影響が強くあらわれる.これに伴う環境の保全や災害対策等を考えるためには,その循環の挙動を数値解析や実測調査を行う事で理解する必要がある.
本研究で対象となる追波湾は東北最大の河川である北上川が流れ込み,湾内の循環はこれに強く依存している(石川・中田,1980).湾にどのように河川水が流れ込むかは上流側での流量だけではなく河口断面や幅によって変化する事は知られているが今まで検討例は少ない.本研究では,マルチレベル流動モデルを使用して,まず出水時の河口幅変化のモデルをいくつか提案し,その違いによって湾の循環がどのように変化するかを解析し,比較検討する.
2. 計算方法
2.1 対象領域・現象
シミュレーションの対象領域・現象は表1にまとめ,図1にその計算メッシュマップを示す.対象期間時の最大流量は約3400トンである.格子間隔は追波湾に向かうほど小さく分割し,深さ方向でも表層を詳細にわけ,深い領域は比較的粗くなっている.ここで,対象となった追波湾の特徴をまとめると,南三陸に位置するエスチャリーであり,表層水は北上川河川水の影響を大きく受け,中層では南および東南からの往復流に影響をうけることが過去の研究より示されている(石川・中田,1980).また,北上川の河川水の流軸は河口から南東の方向で表層を流れるといわれている(石川・小川,1985).
表1 対象領域と現象
| 地域 | 北上川河道(約5km)を含む追波湾全体 |
| 格子間隔 | 水平方向:150m〜500m 鉛直方向:10層(2m〜10mで変化,level10は海底まで) 格子数:44×39 |
| 期間 | 平成13年8月1日0時〜14日24時 |
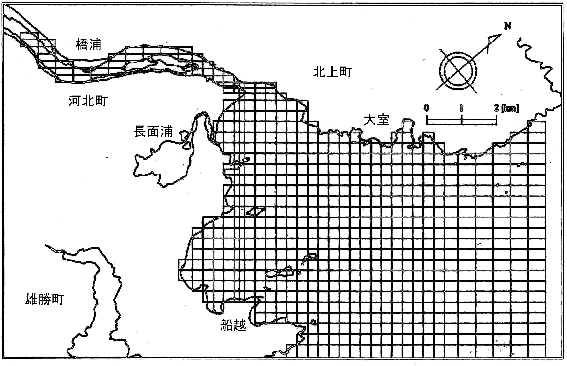
図1. 対象領域の計算メッシュ
2.2 流量モデル(従来のモデル)
(1)砂州回復あり
従来のマルチレベル流動モデルでは,北上川における出水時の河口幅変化を既存の資料を利用して,流量と河口幅との相関を調べ,それで得られた関係式(1)を利用して数値モデルを考えている.以下このモデルを流量モデル(砂州回復あり)とする.
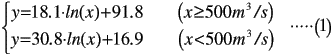
x:流量,y:河口幅
式(1)では,流量が少ないときには河口幅が100m以下と推算されるが,既存の資料から本研究では100mを最小河口幅と仮定した.ここで,流量モデル(砂州回復あり)は長期的データに基づいているため砂州回復過程は考慮しているものの,出水直後の短期間においてこのような回復過程が生じるかどうか疑問が残るところである.
(2)砂州回復なし
そこで,対象期間が短いため河口の回復は大きく変化していないと仮定し,流量モデル(砂州回復あり)を基に今回の出水時の河口幅最大(約239m)で一定としたモデルを設定した.
2.3 流砂量モデル
河口幅が変動する場合,流量の増加により流砂量が増え,これにより砂州が削られるという過程がある.そこで,高木ら(1999)の研究に基づき,Kalinske−Brownの掃流砂式を基に新しい数値モデルを仮定した.以下に流砂量モデルの計算過程を式(2)〜(4)に示す.
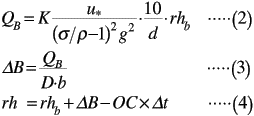
QB:流砂量,K:流砂量補正係数,u*:摩擦速度,σ:砂の密度,ρ:水の密度,g:重力加速度,d:砂礫粒径,rh:河口幅,rhb:Δt前の河口幅,ΔB:砂州変化量,D:全水深,b:砂州幅,OC:砂州の回復率,Δt:計算のタイムステップ
なお,式(2)で与えられる流砂量補正係数Kは対象領域や出水程度により調整する必要がある.
(1)流砂量補正係数K=1.0
まず,K=1.0とした場合を考えた.この時河口幅が500m以上になり,必要以上の量が削られた.実際は河口幅の上限値があり,今回は239mとした.
(2)流砂量補正係数K=0.115
次に最大河口幅を239mとして,流砂量補正係数の値を調整する事でその値を推定した.その結果,K=0.115で再現する事ができた.
以上に示した流量モデルと流砂量モデルそれぞれの河口幅の変化と流量の時間変化を図2に示す.流量モデルは出水の前半から砂州の浸食が大きい事が特徴である.

図2.河口幅と流量の時間変化
3. 結果
2.1と2.2で示した河口幅変化のモデルで追波湾のシミュレーションを行った.その結果,出水時に湾の循環に違いが見られた.特に,大きな違いがあったのは,流砂量モデル(K=0.115)であった.他のモデルでは,湾全体の流れにそれほど大きな違いは見られなかった.流砂量モデル(K=0.115)では, 河口幅が他のモデルに比べて小さいため,出水による河口部の流出速度が速くなっている.この結果,北上川の河川水の流軸が南東方向によるという特徴が,流砂量モデル(K=0.115)で強まっている.図3に追波湾出水時の循環の様子を簡略化したものを示す.出水時は河川水の流出が南東に偏っており,時計回りの循環が大きくなる.この時,流砂量モデル(K=0.115)は,他のものと比べて河口付近の循環1で強くかつ密度が高くなり,船越湾の循環3で強く密度が低くなる結果となった.出水後流量が減少していくと湾の状態は,同じような循環形態をとっており各モデルで違いが見られなかった.
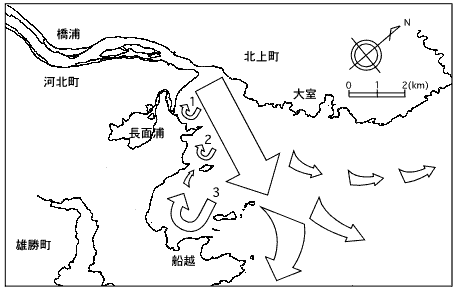
図3.追波湾での出水時の循環形態
4. まとめ
本研究で仮定した4つのモデルより,その河口幅変動の違いは出水時の影響の違いに現れ,それは追波湾の流れの特性が大きくなる事で確認された.
しかし,本研究で仮定した流砂量モデルにおいて,流砂量補正係数や砂州の回復率で実測値との比較やその値の取り扱い方で更に検討が必要である.
謝辞:本研究の実施にあたり東北整備局北上川下流工事事務所にはデータ提供で協力を得た.ここに記して謝意を表す.
参考文献
- 石川公敏・中田喜三郎(1980):追波湾の海域特性(Ą),公害資源研究所彙報,第9巻第4号,pp.35〜45
- 石川公敏・小川利郎(1985):追波湾の海域特性(˘),公害資源研究所彙報,第14巻第3号,pp.45〜57
- 高木利光・増田巧見(1999):簡易モデルによる中小河川の砂州フラッシュ予測,河口研究NO5,pp.7-1〜7-4
御意見・御質問は以下へ.
