1. はじめに
津波は沖合から沿岸部に達すると，全水位が低下し流速値が増大することにより，常流から射流へと遷移をする場合もある．沿岸部での津波は，波としての性質よりも流れとしての性質の方が強く複雑な挙動を有し，従来の数値モデルでは再現できないという問題を残している．
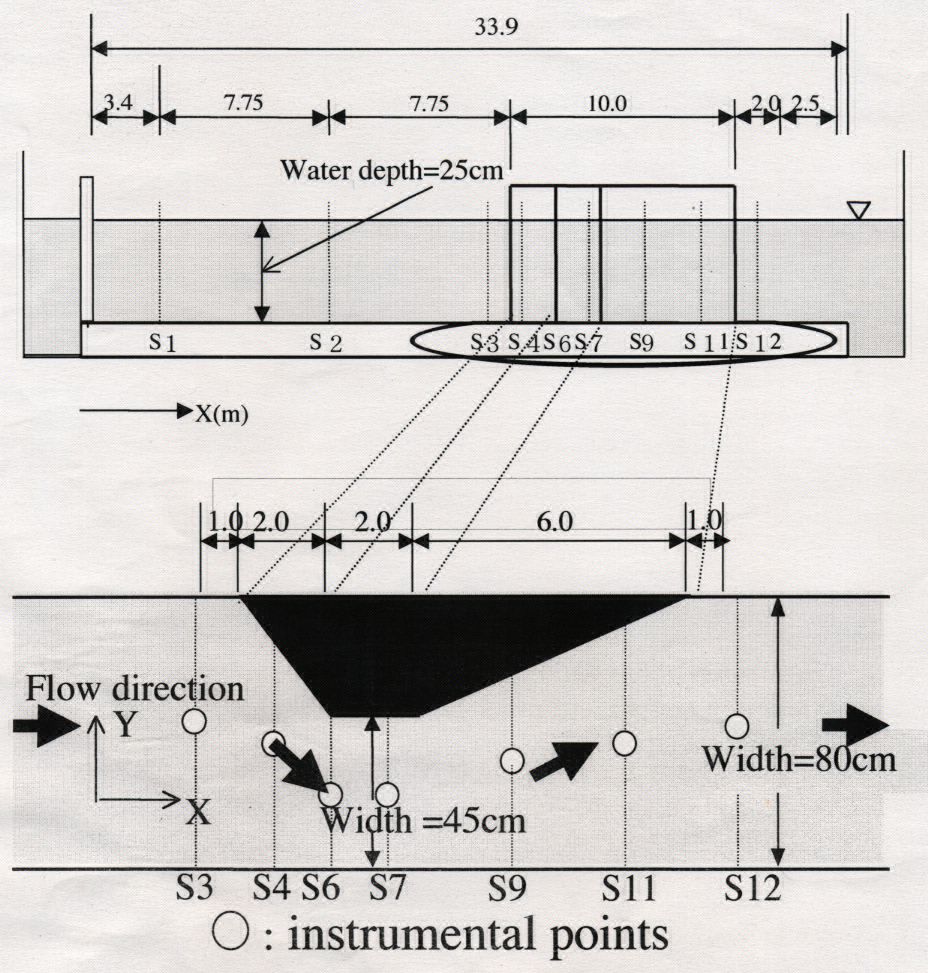
本研究は従来の津波数値計算を改良し，図-1のような実験水槽に対して遷移流が再現できる数値モデルを提案する事により数値計算精度の向上を目指す事を目的としている．
2. 浅水理論式による数値計算
2.1. 移流項の検討
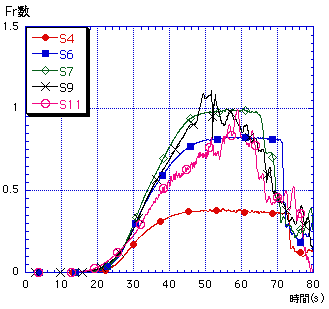
本実験再現計算では，幅方向の分布を考慮しない平面一次元計算では遷移流を再現できるが，平面二次元計算ではなぜか再現できないという問題点が指摘されていた1．ここでFr数が１を越えているのは六計測点のうちS9地点のみであり（図-2-a参），下流端境界に近いS11地点においては両者共に実験値と良い一致を示している．常流状態においては下流側から決定される水位値が非常に重要になってくるため，遷移流を再現する為には少なくとも射流になっていないS7地点より下流側，すなわち漸拡部付近における再現計算精度が良くなければならないのが分かる． 漸拡部では実際に跳水が生じており，その挙動は複雑である為，このような条件下においては非線形長波理論を用いなければ流速値を精度良く再現できないことが分かっている．ここで従来使われてきたモデルの非線形項である移流項に着目すると，一次精度の風上差分を用いており，数値粘性によるなまりが影響してしまう可能性は高い．よって，より高次精度の計算を行える差分スキームに変更をする事により，数値粘性が低く押さえられ，移流項が正確に効いてくる流れを再現できる期待を持てる．これらより本研究では，三次精度の風上差分を用いて計算を再度行う事とした．これに用いるスキームを(1)式に示す．
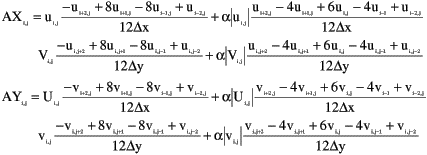・・・・(1)式
・・・・(2)式
ここで(1)式において(2)式のようになり，αは定数で1.0の時UTOPIAスキーム，3.0の時にK-Kスキーム（河村スキーム）となる．α=1.0の形がもともとであるが，人為的に安定性を増加させるためにUTOPIAの人工粘性を３倍にしたものが河村スキームである2．本数値計算ではこの河村スキームを基に，次の時間ステップのM,Nを求める形に変えたものを用いる事とする．
2.2 三次風上差分を用いた数値計算
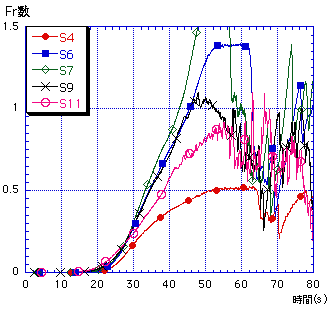
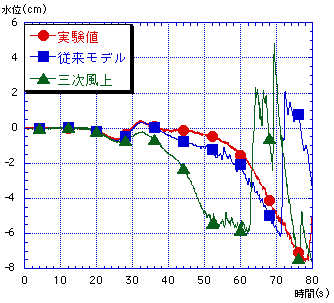
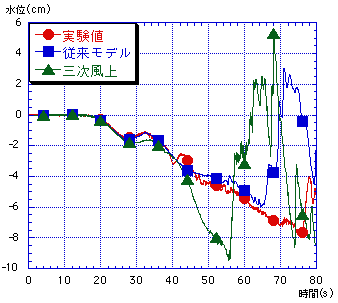
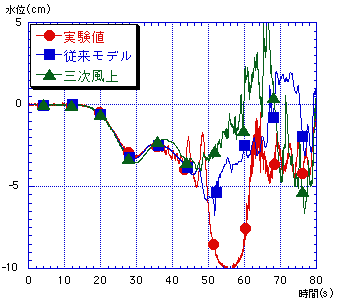
三次精度風上差分は(1)式から分かるように，2格子まわりの流量を用いる為，壁付近及び上流端下流端境界においては，計算領域不足の為用いることが出来ない．よって，そのような場所については従来通りの一次精度の風上差分を用い，三次精度と一次精度の二つの計算領域に分けて移流項の数値計算を行えるようにプログラムを組む．また，今まではΔx=10cm,Δy=5cm,Δt=0.01sによって数値計算を行っていたが，これだと横断方向に17メッシュにしか分けられず，三次精度の計算が行える領域が狭くなってしまう為，より細かいΔx=2.5cm,Δy=2.5cm,Δt=0.0025sのメッシュサイズによる計算を行い従来のモデルと比較をすることにした． ここで限界流が生じるポイントである特異点を通るような流れにおける水面形状を考えると，�@水路床勾配，�A水路幅，�B摩擦の影響，�C流量の変化の四つの要素によって決定される．この中の摩擦の影響，すなわちマニングの粗度係数nについて，本数値計算では津波の数値計算に良く用いるn=0.025(s/m1/3)を導入していたが，実際の実験においてこのような係数をとっていたかどうかは特定できなく，また流速値が実験値に対して過小評価されていた為，下流での水位の条件を上流側に生かすために水位の減衰は小さいものとし，n=0.0 (s/m1/3)とした． これらによる数値計算結果のうち，S6,S7,S9の三点についての水位を図-3に示す．また遷移流の検討を行うために，実験値・従来モデル・三次風上モデルについてのFr数の時系列変化を縮流部における計測点５点について求めた．これを図-2にそれぞれ示した．これにより，三次風上では狭窄部に位置するS6,S7地点において水位の低下，流速の増大により遷移流が大きなFr数で起きているのが分かる．しかし実験値とは大幅なずれが見られ，現況では一次風上の方がS9地点における大きな遷移を除けばむしろ実流況に近い再現が出来ている． 三次精度風上差分は(1)式の様なu,vを用いた形で行うのが一般的である．Eulerの式を水深積分化した浅水理論における差分スキームは，分母に4点の全水深を用いるなど複雑な形をしている為，二格子周りの流量を用いる三次風上差分に対してこの形を適用すると，更に式の形が複雑になる．よって，計算の不安定化を招きやすいと言える．
2.3 境界条件の検討
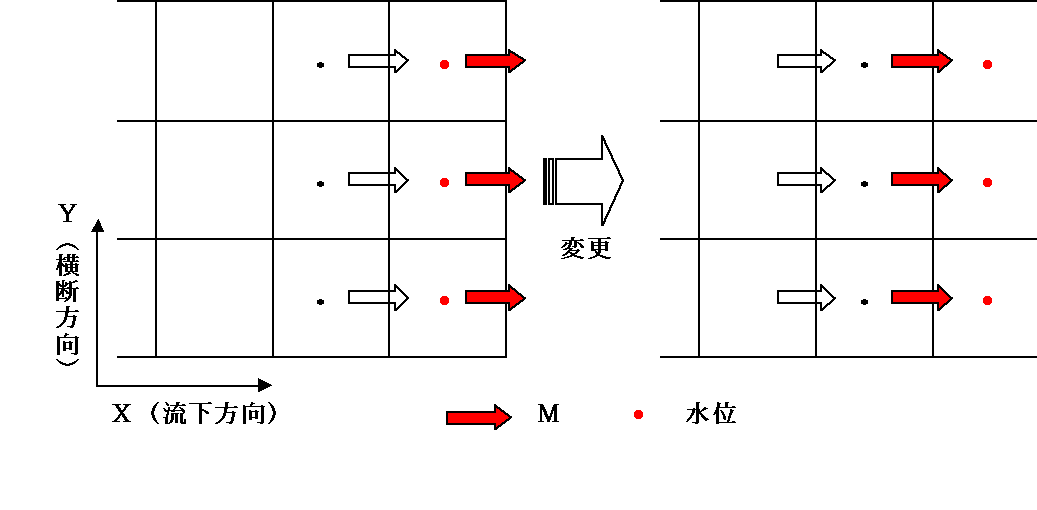
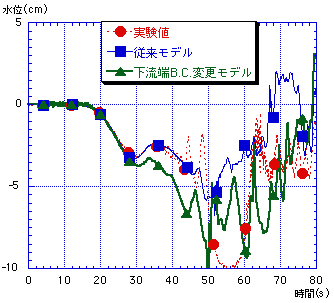
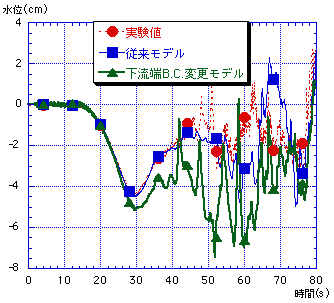
ここで下流側の境界条件に着目すると，本数値計算は水位と流速を強制入力させている．現況の津波数値計算モデルでは，水位の下流での情報は運動量の式で扱われるが，流速の情報はスタガードメッシュのために連続の式で取り入れられず，この流速の条件が良好に取り入れられていないのが本数値計算の問題点として挙げられる．このような下流での情報が良好に取り入れられない中で，移流項を多メッシュに渡って用いてしまった事が図-2-cのような結果を招いたと考えられる．ここで下流の流速の情報を上流側二反映させる為に図-4の様な境界条件の変更を行い，再度数値計算を試みた．これによる数値計算結果のうち，S9,S11地点についての水位時系列変化の様子を図-5に示す．この図より，S11地点での水位の過小評価がS9での水位の低下につながっており，従来モデルの方が良好な再現が出来ていると言える．
3. おわりに
本実験再現計算は常射流混在流であり，解析は非常に複雑で難しい．常射流混在流に対しては過去に色々な試みで数値計算がなされているが（例えば河村ら(1993)3），下流側の境界条件が水位流速強制入力のケースについてはなされていない．よって，本実験の再現を良好に行うには下流側の条件を良好に反映できるモデルが必要とされよう．
参考文献
