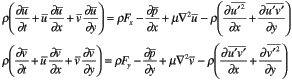1. 　はじめに

津波は沿岸部に達すると，急縮効果などにより水位が低下し流速が増大する事があり，常流から射流に遷移すると言われている．沿岸部における津波は，波としての性質よりも流れとしての性質の方が強く複雑な挙動を有し，現況において遷移流を再現することは困難とされている．本研究は，遷移流を起こす水理実験結果に対して，浅水理論式に水平拡散項を付加することによって数値計算された結果を比較し，遷移流を再現できる数値計算モデルを検討することを目的としている．

2. 　浅水理論式による数値計算

2.1.　遷移流の実験及び再現計算の現況

　佐々木(1999)1は，図-1のような実験モデルにおいてStaggered Leap-frog法を用いた浅水理論式による数値計算を行ったが，平面一次元モデルでは遷移流を再現できるが平面二次元モデルでは水位が下がらず流速が過小評価されてしまったために，遷移流を再現できないという問題性を指摘した．遷移流は狭窄部から下流部へ少し離れた地点S9において実験計測されている．遷移流が起こらない原因は主流の幅方向の再現性にあり，拡幅部壁付近におけるよどみ域が大きいために横断方向の流れの広がりを遮ってしまったためである．佐々木(1999)は問題の解決方法として，格子間隔を変化させたり，また倍精度実数計算を行うことにより，打ち切り誤差及び離散化誤差，境界近似誤差，丸め誤差を検討したが，問題となっているS9において射流状態が再現されることはなかった．

2.2.　遷移流の起こらない原因

　2.1.より，遷移流の起こらない原因は支配方程式であることが分かった．過去に富澤ら(1990)2に行われた研究では，急拡部水路において剪断渦が生じる拡幅部では水平拡散効果が無視できなく，水平拡散項を支配方程式に取り入れる必要性が報告されており，本実験モデルは漸拡水路であるが，急拡水路と同様の考慮が必要であることが分かった．

3.　水平拡散項の浅水理論式への導入

3.1 レイノルズ応力に関する仮説

　2.2で述べたような拡幅部において剪断渦を伴う剪断流，すなわち自由乱流運動を数値計算に新たに取り入れるには，それに伴うレイノルズ応力を考慮しなくてはならない．浅水理論式は，Eulerの式を静水圧仮定のもと鉛直方向に底面から水表面まで積分した事によって導かれたものであり，粘性項は考慮されていない．水平拡散項を取り入れた数値計算モデルを導入するには，Navier-Stokesの式が必要である．時間に関しての平均値と変動分の和で表した流速を，二次元のNavier-Stokesの式に取り入れて整理すると，次のレイノルズ方程式が得られる．

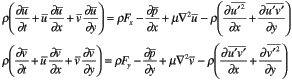　　　　　　　　　　　　　　　　　　　　　　　　　　　・・・・(1)式

上式において，右辺第四項がレイノルズ応力を含む項である．レイノルズ方程式を解くためには，レイノルズ応力のモデル化が必要とされる．その中で元も単純な考え方が，流れの平均流速分布と関連づける仮説を立てるものであり，ブシネスク(日野,1992)4はレイノルズ応力を次のように表現した．

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ・・・・(2)式

(2)式でεは渦動粘性係数であり，［長さ］×［速度］の次元をもっている． 従って，水平拡散係数としての渦動粘性係数を導入すれば流れの幅が広がり，本再現計算で問題となっている漸拡部におけるよどみ域の拡大も解消される可能性が期待できる．

3.2.　遷移流の数値計算

浅水理論式における運動方程式に水平拡散項を付加し，再現計算を行うにあたって以下の二次元についての微分方程式を数値計算する．

　　　　　　　　　　　　 　　　　　　 　・・・・(3)式

εx1,εy2については，まず一定値を仮定する．一方ε_x2,ε_y1については，渦動粘性係数は自由乱流では流下方向に垂直な断面内で一定で，それは噴流や後流の断面内の最大最小流速の差とその幅bとに比例すると仮定するPrantle(1942)の第二の仮説に基づいて以下の式を導入する．　

　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　 ・・・・(4)式

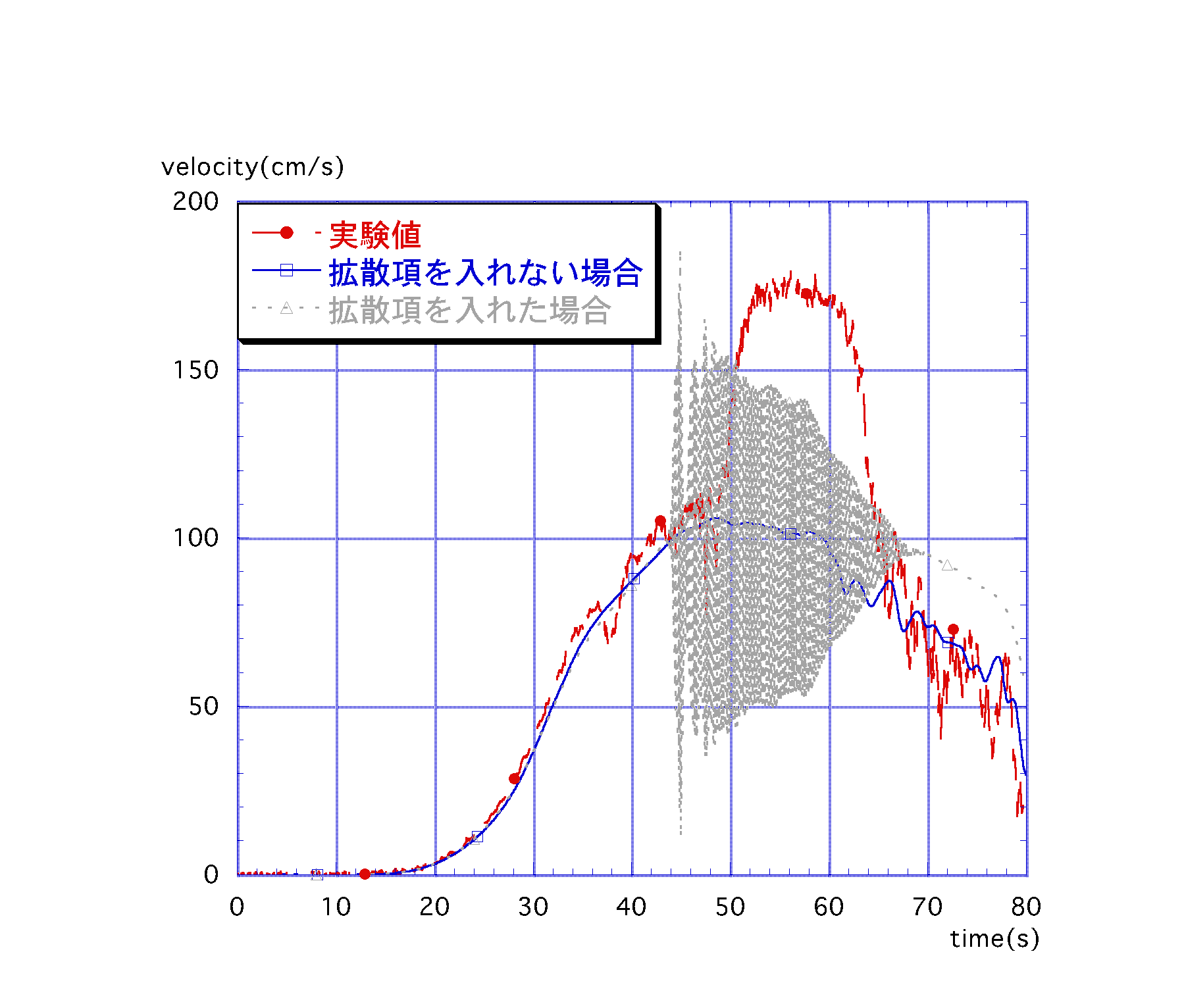
b(x)については漸拡に伴う噴流の幅の広がりに期待し，水路幅を入力する．k₁は1/Re_ε(Re_ε：乱流レイノルズ数)で定義されるが，この値は詳細な実験データをもとに決定されるべきものであるため，現時点では決められないのでRe_ε=2000と仮定してk₁=0.0005とした．図-2,図-3にε_x1=0.39(m²/s),ε_y2=0.05(m²/s)として，ε_x2及びε_y1に(4)式により求められた拡散係数を導入する事によって得られたS9地点における水位及び流速値を，実験結果及び浅水流方程式による計算値と比較させたグラフを示す．
　図-2,3より，拡散係数を導入したことにより水位が下がり流速値が大幅に上昇しているのが分かるが，数値振動を起こしてしまっており，この振動はεx1及びεy2の値による影響が強く，値を大きくするほど振動幅が大きくなっていき，これ以上に二つの拡散係数を大きくすると発散してしまうことが分かった．

3.3.　幅方向にも分布を持った拡散係数

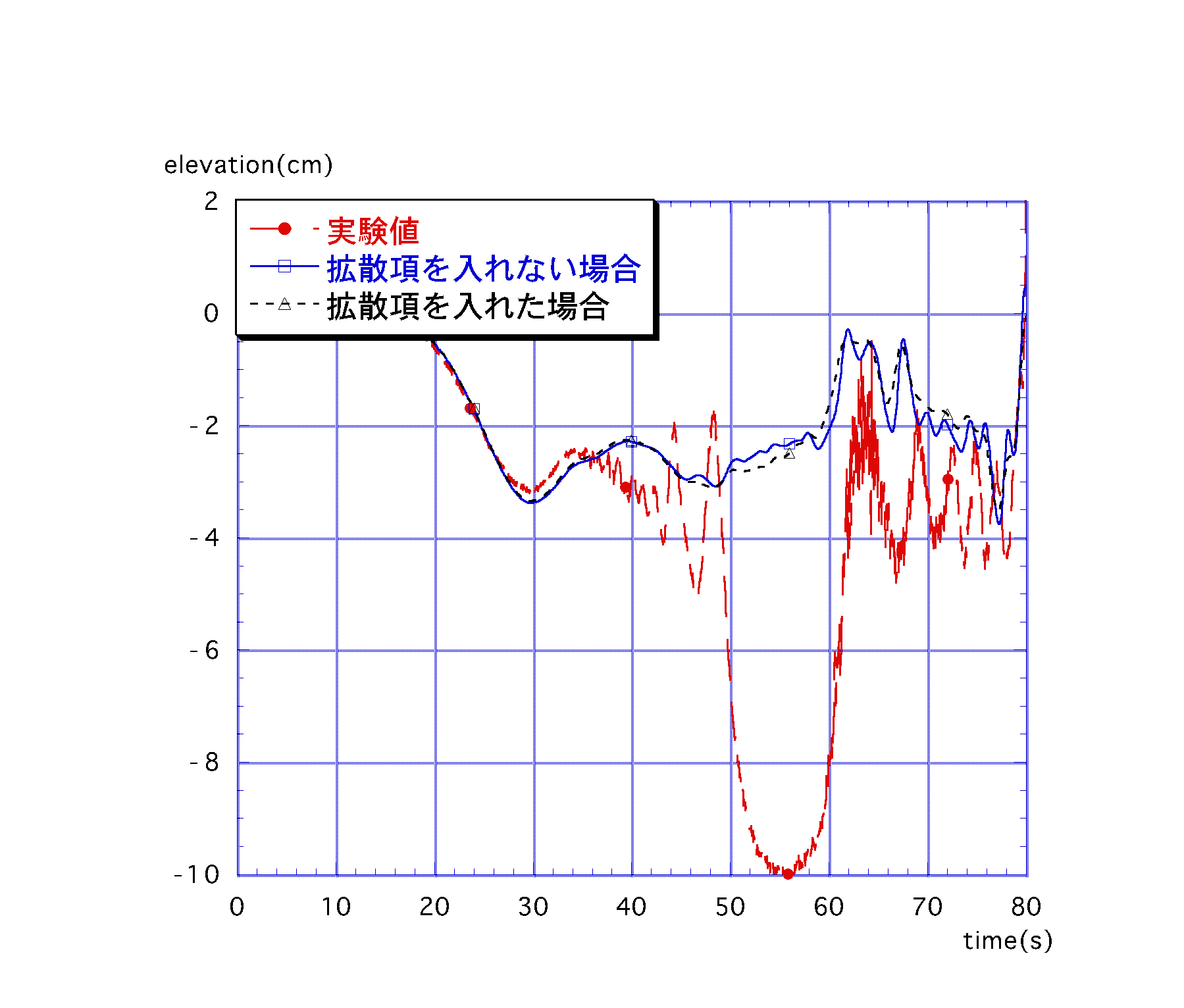
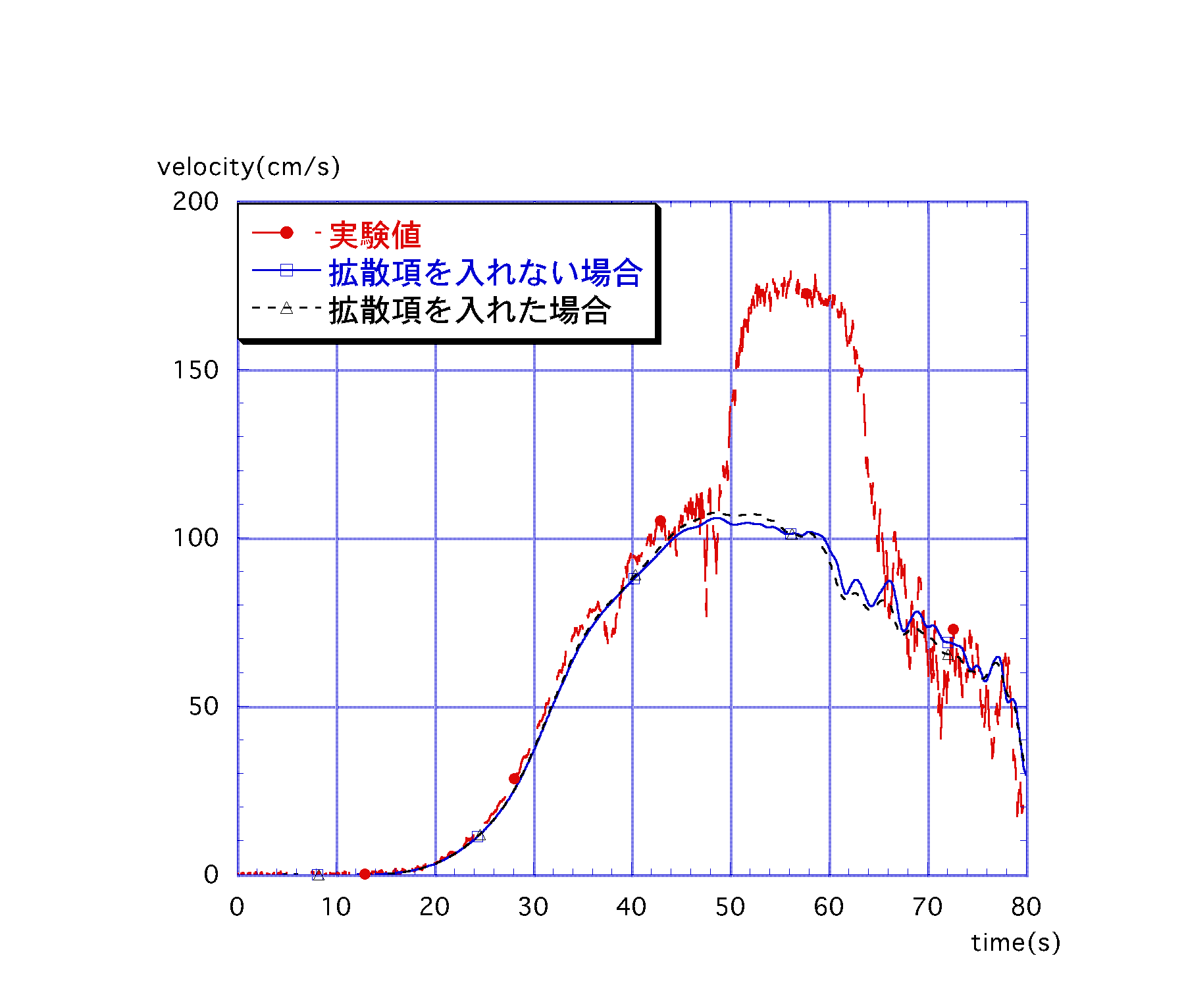
　富澤ら(1990)は，急拡を伴う水路実験において急拡部での運動量の水平拡散効果を検討するのに，水平拡散係数を実験における流れの平均値から見積もっている．これにより自由噴流域内では｜du/dy｜に比例するという関係が得られており，本研究モデルにもこの要素を取り入れる事にした．
　この事によって渦動粘性係数は幅方向にも分布を持つ関数となる．計算結果を図-2,3と同様に比較させたものを図-4,図-5に示す．今度は数値振動は起きてないものの，水位及び流速の改善は顕著に見られなかった．

4.　結論及び今後の課題

　渦動粘性係数は場所によって分布を持つ関数であり，急拡を伴う水路においては偶角部で最大値を取るような分布になることが過去の研究より指摘されており，本モデルではこのような分布は得られていない．従って，数値振動が起こってしまう又は遷移流が起こらないような現時点での拡散係数では，実験値のような結果は得られないことが分かった．水平拡散項を取り入れたモデルは，本実験モデルのみでなく沿岸部における津波の数値計算にも適用できるようなものでなければならない．従って今後は，林(1997)3が行ったような水深平均k-εモデルを用いた解析が必要とされ，普遍的な渦動粘性係数を求められるようなモデルが本実験計算にも必要とされる．今回の研究によって遷移流は引き起こせなかったが，水平拡散項を浅水理論式に付加することにより，水位が下がり流速値が上昇するという可能性を示すことは出来た．

参考文献

1. 佐々木洋之(1999)：遷移流における数値計算精度の検討，
   　 　　　東北大学卒業論文，pp.1-66
2. 富澤　大・今村文彦・首藤伸夫（1990）：急拡部を通過する津波の水理特性，
   　　 　　海岸工学論文集 第37巻，pp.131-134
3. 林雄一郎(1997)：急拡を伴う非定常流れの数値解析，
   　　　　東北大学修士論文，pp.1-39　
4. 日野幹雄(1992)：流体力学，朝倉書店，
   　　　　pp294-300,pp330-332
   

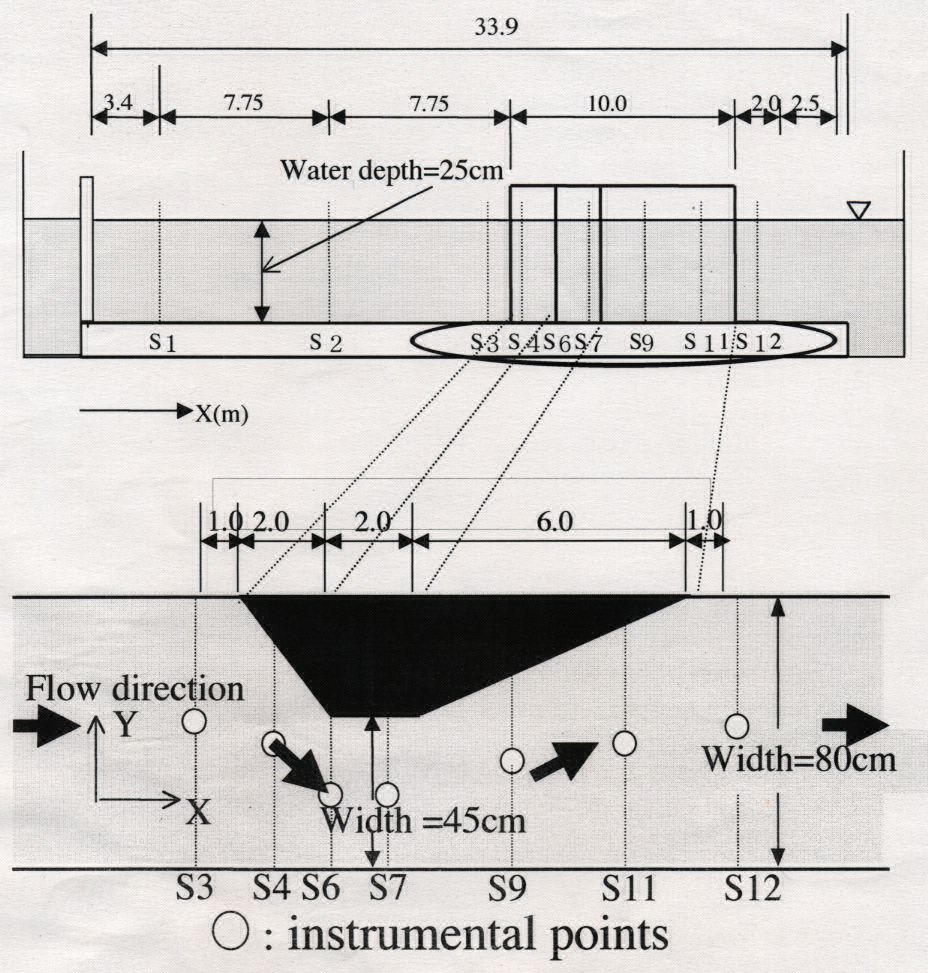
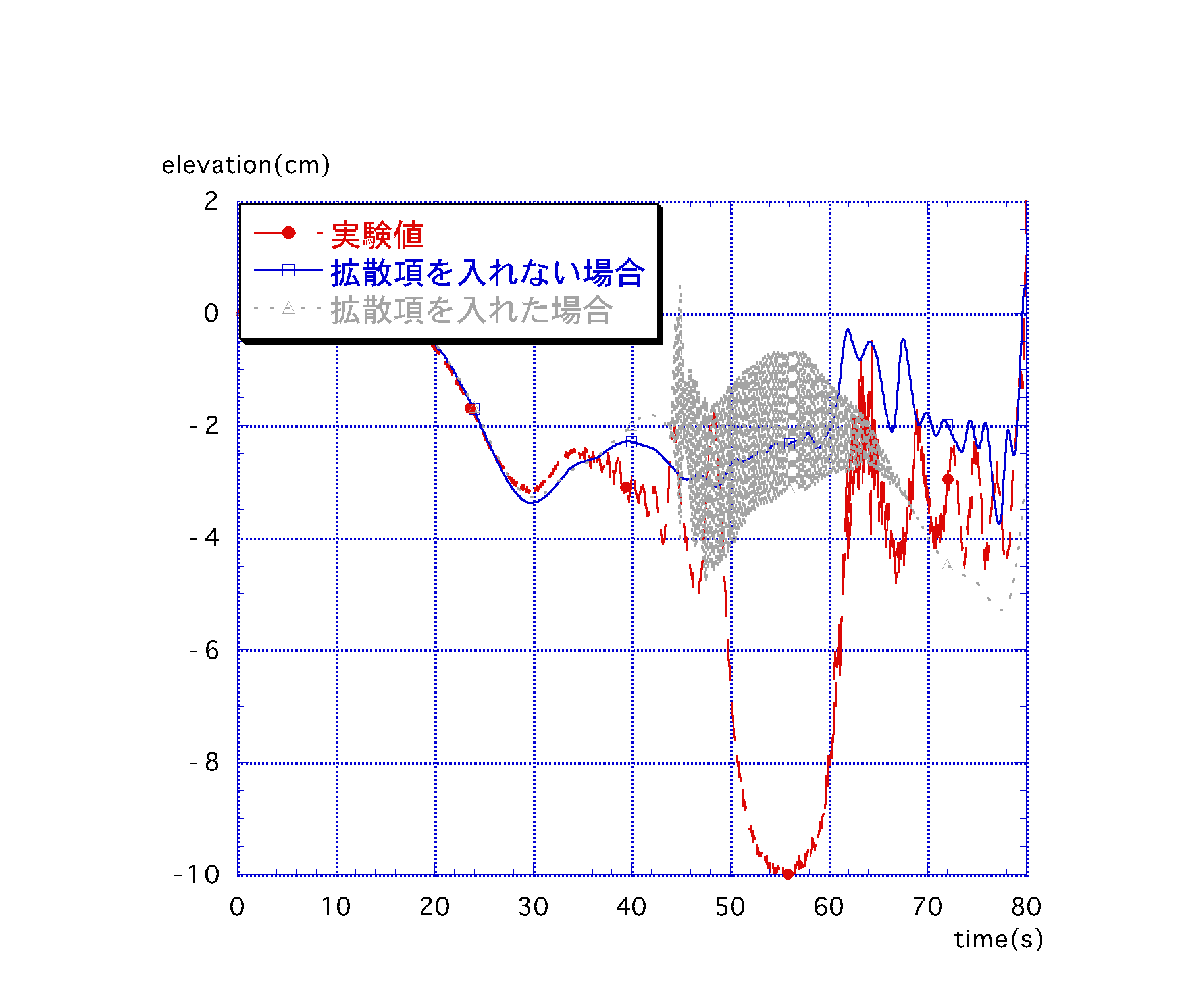
図-2　 拡散係数導入（3,4式）によるS9における水位