1. はじめに
津波は長波であるため,沖で砕波することはないが,浅海域では地形条件な どにより砕波現象が起こる場合もある.実際,1983年日本海中部地震津波では,ビデ オや写真で先端波形がくずれた津波の様子が記録されている.砕波が起こるとエネル ギーが減衰し,陸上での遡上高さに影響されることが指摘されている.このような砕 波現象を考えることは,津波数値計算で正確な遡上高さを算定する上で重要である. 砕波現象は,浅海での分散効果も含めて議論する必要があり,本研究では,このよう な現象の基礎検討を行うことを目的とする.
2. 実験と計算の比較検討
2.1 実験の概要
砕波の数値計算を検討するにあたって,実験値との比較をする必要がある. 砕波に関する既存の実験として,原田(1998)1 の行った実験結果があり,これと比較する.水理実験装置をFig.1に示す.実験は,ゼロアップ・ゼロダウンクロス間平均5.5 秒,最大波高平均12.4cmの孤立波を1波発生させている.波は1/5勾配において前傾化 し,分裂が始まり,高水路部において砕波に至る.これをX=0mから順に1m間隔で計測 されている.本研究では,このうちX=0‾20地点のデータを参照した.
2.2 計算方法
浅水理論をStaggered Leap-frog差分法で計算する.格子間隔0.1m,時間間隔0.01秒,格子数を伝播方向 200,幅方向15とし,拡張性を考えて2次元プログラムを用いて,実験水槽内での距離 20mを1次元伝播計算した.ここで,境界条件はX=0で実験波形の水位,流量を強制入 力とし,もう一方を自由透過,水路両岸を鉛直壁とした.
2.3 計算結果
幅方向の軸をJとして,壁面の影響の少ない中央のJ=7での時間波形を採用し ,水理実験との比較を行った.この結果をFig.2に示す.
この結果を見ると,数値計算において波先端における波形勾配の増加や,段 波,海底摩擦の表現による波高の減衰は現れている.しかし,予想されるとおり分散 性や,X=7m付近にかけて実験で起きたとされる砕波は表現できていない.その結果と して,波高の大きな増大,減少が起きず,少しづつ減少していく.また,空間波形に ついても同様である.
3. 砕波地点の決定について
3.1 決定方法
砕波減衰を,まず砕波地点を知り,その先に減衰項を入れることを考える. 砕波地点の与え方には,波高水深比と位相速度に対する表面水粒子速度us/C(ここで ,us:表面水粒子速度,C:位相速度である)の大きく2つがあるが,このどちらも合田 (1973)2の砕波指標を元にしたものがよく用い られている.前者は,沖波の条件で決められるため波が沿岸近くで複雑に変形する場 合には適用できない.津波もこれと同様であると考えられるので,ここでは後者を用 いる.
3.2 結果
計算で考えているのは浅水理論なので長波近似を用いているが,砕波を考え るので表面水粒子速度をよりよく表す意味で,ブーシネスク方程式の近似を考える. それぞれ,長波理論ではÈ,É式,ブーシネスク近似度ではÊ,Ë式を用いて求めこ とができる.これらの結果を空間波形とともにFig.3に示す.
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
ここで,us:表面水粒子速度,u:平均断面流速,D:全水深,h:水深,η:水位 ,C:位相速度(波速),g:重力加速度である.
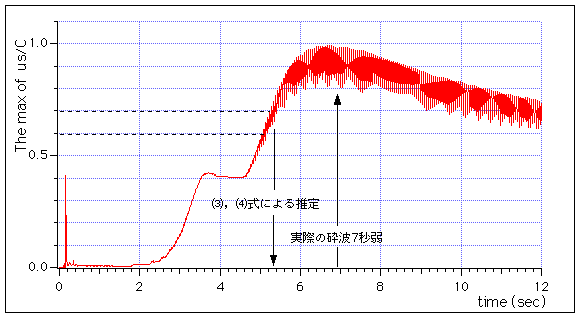
Fig.3を見るとus/Cは長波のものでは空間波形に対応 した値となっており,一方ブーシネスク近似度のものは波の先端近くで値が大きくな っている.これは波が前傾化されている効果と思われる.また,後者の結果を各時間 での空間最大値をFig.4に示した.片山・佐藤(1993)3を参考にus/Cが0.6〜0.7である時間を見ると,砕 波はほぼ5秒で生じており,実験の7秒弱のものと一致しない.
浅水理論を用いた数値計算結果を利用して,簡易的な砕波指標の提案を試み たが,È,É式を用いた場合過小評価であり,Ê,Ë式を用いた場合過大評価である ことが分かった.特に,È,É式を用いた場合,us/Cが砕波地点に近づいても増加し ない傾向があり,砕波地点の推定が難しいことが分かった.
4. おわりに
今回,浅水理論を用いた計算での砕波指標の検討を行った.今後は,砕波減 衰項の導入とブーシネスク方程式で同様の検討を行う予定である.
参考文献
1) 原田賢治(1998):波状段波の砕波前後における水理特性に関する実験,東北大学 卒業論文,p.40.
2) 合田良実(1973):防波堤の設計波圧に関する研究,港湾技術研究所報告,第12 巻,第3号,pp.31-69.
3) 片山・佐藤(1993):Boussinesq方程式を用いた不規則波の浅水・砕波変形の計 算法,海岸工学論文集,第40巻,pp.16-20.
Fig.1 水理実験装置
Fig.2 各地点での時間波形の比較(実線:実験値、点線:計算値)
Fig.3(左から順に)t=2‾7秒の空間波形とus/C(上から水位、長波理論による us/C、ブーシネスク近似度によるus/C )
Fig.4 ブーシネスク近似度によるus/Cの各時間での空間最大値