東北大学工学部　学生員　○琴浦毅

1 はじめに

台風などの強降雨時の出水時における流出解析を精度よく再現するためには，流域全体で地下への浸透を考慮に入れた計算が必要となるが，これを2次元的に計算すると計算量が膨大になり実用的ではない．本研究では一級河川である阿武隈川全流域を対象とする出水における流出解析に組み込むことを目的とした，地下水流動を鉛直下方への浸透と側方流動を分ける計算方法を開発し，その妥当性を検証する．

国土数値情報により擬河道網を作成し，山地斜面，平地斜面，河道に分類し，地下水流は山地斜面のみで起こると考え，表面流出はkinematic wave法，飽和地下水流出はダルシー則，地下への不飽和鉛直浸透はダルシー則を不飽和領域まで拡張したRichardsの式を用いて計算する．

山地斜面の各メッシュにおいて図1のように座標系を定義し，(x，z)方向流速を(u，w)，土壌水分含水率をで表すと連続の式は

　　　　　　　 (1)

となり，この連続式を(x，z)方向に分解して計算し，

方向の不飽和浸透計算の結果を方向の計算結果により補正するものとする．

　

図1　座標系

方向浸透のみを考え側方流動を無視した場合の土壌水分含水率をθ₁と定義すると，θ₁は以下の

3式((2):Richardsの式, (3):Brooks & Coreyの表示法，(4):Cambellの表示法)により求められる．

　　　 (2)

(3)

　　　　　　　 (4)

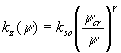
　ここで，Ψは圧力水頭，k_z(Ψ)は不飽和透水係数，θ_sは飽和体積含水率，θ_rは最小体積含水率，k_soは飽和透水係数，Ψcrは限界圧力水頭，γ，λは定数である．

x方向浸透のみを考えた場合の土壌水分含水率をθ₂と定義すると，θ₂は側方浸透にx方向の変化があることによって生じる分布で，しかも飽和浸透層内での浸透なのでθ₂は飽和面近くで有意である．

θはθ₁の形を変えないで，方向にc_g dtだけ平行移動しただけとすると

　(5)

両辺で除す事により(5)は以下のようになる．

　(6)

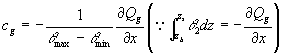
ここでQ_gは地下水飽和側方流量で，これはダルシー則(7)から求められる．

　　　 (7)

　　　　　　　　　　　　　 (8)

　以上の結果を用いて水分量変化を補正する．

　　　　　　　　　　　　　　(9)

(8)から方向土壌水分量分布を得て，地下水面の位置を決定する．

　

図2　地下水計算フローチャート

各メッシュにおいてkinematic wave法を用いて，擬河道網を通じて河口まで追跡計算する．任意断面形状の流路における洪水移動速度を表すKleitz & Seddonの式を利用すると支配方程式は次式になる．

(10)

ここで，wは洪水の移動速度，Qは流量，tは時間，xは流下方向の距離，yは水深方向の距離，Aは流域断面積，Bは水面幅，B_slは降雨を与える幅である．

等流を仮定すると，A，Bはマニングの公式を用いてQを使って表現できる．この式を差分化して流出計算を行う．

今回開発した手法を1998年8月の出水に適応し，地表流のみを計算する以前までの手法(model1)と本手法(model2)を比較，考察するために福島における計算値を図3に観測値を加えて示す．この出水では流量ピークは2回存在するが，model2は地下水流を計算するために地表流が減少した後も地下水流出が継続し，谷部においてmodel1より流量が多くなり比較的観測値に近くなっている．また，降雨が全て流出に寄与するmodel1に対し，model2は降雨の地中への浸透計算を行うため地中に浸透する降雨成分が存在し，その結果降雨変化に対する流出変化がmodel1は非常に敏感であるのに対しmodel2は緩やかになっている．また，地下水流量は地表流ほど早期に減少しないため観測値ではピーク後の流量減少は比較的緩やかに推移するが，地下水流量を計算するmodel2の方がmodel1より流量減少が観測値に近いのが分かる．

しかし，model2と実測値を比較するとまだピーク到達時間，ピーク時流量など完全に再現されていないと言える．

　

　

図3　計算値と実験値との比較