 図−1
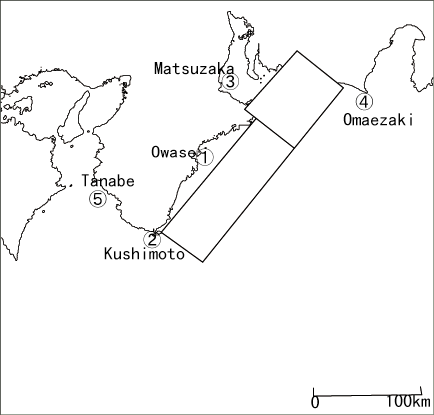
図−1Wavelet変換を用いた津波初期波形の推定
東北大学 正会員 ○小池 信昭
東北大学 正会員 今村 文彦
現在,津波危険度の事前評価および津波警報ための数値予報では,数値シミュレーションによって解析する方法が主流となっているが,その初期条件として用いられる波源は津波の観測によって得られた値を用いるのではなくて,地震断層モデルから計算される鉛直地盤変位がそのまま海面の変動量になると仮定して与えている.しかし,断層モデルは断層運動の第1近似モデルであり,さらに地盤の変位がそのまま海面に与えられることを仮定しているので,このような初期波形が実際の現象とどの程度一致しているのか疑問である.実際,津波の初期波形そのものの観測例がないため,その問題が検討されていない.しかし,初期波形そのものを観測することは今だ難しいので,津波の検潮所などの観測値から初期値を推定するインバージョン法によって,津波の初期波形を推定する手法が必要であり,本研究はその確立を目的とする.
通常の津波インバージョン手法(Satake,1989)は,まず断層面をいくつかのブロックに細分化し,それぞれについて単位すべり量を与えたときの地殻変動を求める.これを初期値として,実際の地形について津波の伝播を計算し,検潮所での波形をグリーン関数とする.i番目の検潮所における,断層面上のj番目のブロックからのグリーン関数をAij(t)とすれば,観測波形bi(t)は各グリーン関数を各ブロックのすべり量xjを重みとして足したものであるから,
Aij
(t)・xj=bi(t) (1)と書ける.これは連立方程式であり,最小二乗法でとけて,各ブロック上でのすべり量
xjが求められる.しかし,これでは断層面を仮定していくつかのブロックに細分化しているためその位置を仮定していることになる.そこで,ここでは断層面の変位だけでなく,その位置も推定できるように,次のように取り扱うことにした.
まず,計算領域全体で
wavelet基底を初期値として,実際の地形について津波の伝播を計算し,検潮所での波形をグリーン関数とする.i番目の検潮所における,j番目のwavelet基底からのグリーン関数をAij(t)とすれば,観測波形bi(t)は各グリーン関数を初期波形のwavelet展開係数xjを重みとして重ね合わせたものであるから,先程と同様に,Aij
(t)・xj=bi(t) (2)と書ける.この連立方程式を解いて初期波形の
wavelet展開係数xjがもとめられる.結局求めるべき津波の初期波形ηは,
wavelet基底をηjとして,η=
x1η1+x2η2+…+xnηn (3)で求まることになる.
これまでの津波インバージョン手法との違いは,すべり量を直接的に推定するのではなく,まずwavelet展開係数を推定し,それを用いて,津波初期波形の位置とすべり量を同時に求めている点に特長がある.
ここでは,実際の観測値を使う代わりに数値シミュレーションとして,1944年東南海地震の断層モデルを用いて初期波形を計算し,それから津波の伝播計算を行い,図−1の各検潮所で計算される波形を観測値の代わりとして用いることにした.そして,それからインバージョンとして求められる初期波形が,1944年東南海地震の断層モデルから計算した初期波形とどの程度一致するかを検討する.
最終的に式(3)を用いてインバージョンによって推定された津波初期波形を,1944年東南海地震の断層モデルから計算した初期波形と比較したものを図−2から図−5に示す.これらの図では,黒の濃い部分が変位が大きく,薄い部分が小さい.なお,ここではwaveletとして,他のwaveletと比べて波長の長いBaylkin(斉藤,1998)のwaveletを用いた.
 図−1
図−1求めるべき初期波形である図−2と計算結果の図−3を比べると,まわりにノイズが生じているものの,断層の位置は比較的正確に推定されていることがわかる.ノイズが生じている原因として,逆行列を解くとき十分な数の検潮所のデータが得られなかったことが考えられる.また,図−2において,断層の下半分は,黒が濃く変位が大きくなっているが,図−3においても,同様の部分で黒が濃くなっていて,変位が大きくなっていることがわかる.図−4は図−3と大きく変わらない.また,図−5では,データ数も増えてノイズも少なくなり,推定された初期波形の形も,もとの断層モデルの形に近づいていることがわかる.
 図−2
図−2
 図−3
図−3 図−4
図−4
 図−5
図−5また,初期波形の再現性を相関係数で評価すると表−1のようになる.これから,図−3と図−4があまり違わないこと,また図―5の方が図−3および図−4よりもかなり再現性がよいことがわかる.
4.おわりに
表−1では,検潮所の数が5つの場合では,4つの場合よりも相関係数が低くなってしまっている.これは,検潮所の位置が関係していると考えられる.検潮所の位置がインバージョンにどのように関わっているかは,今後の課題である.
| 検潮所の数 | 相関係数 |
| 2 | 0.529 |
| 3 | 0.530 |
| 4 | 0.840 |
| 5 | 0.626 |
参考文献
Satake,K. (1989) : Inversion of tsunami waveforms for the estimation of heterogeneous fault motion of large submarine earthquakes, J.Geophys.Res., Vol.94, pp.5627-5636.
斉藤兆古
(1998):ウェーブレット変換の基礎と応用,朝倉書店,p.214.御意見・御質問は以下へ.
