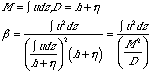従来,防波堤・防潮堤などの人工構造物により沿岸地域を津波から守ってき た.しかし,建設や維持メンテナンスの費用がかさみ,さらなる整備は難しい.その 中で近年,環境問題とも関係して防潮林などの自然を生かした方法の見直しが計られ ている.そこで,本研究では,防潮林としてマングローブを取り上げ,これをモデル 化し水理実験を行った.これにより,マングローブの津波に対する抵抗特性を検討し た.
2. 実験方法
実験は屋外実験水路を用いて行った.水路は全長100m,幅1mのコンクリー
ト製の二次元開水路で,水路端から17.5mは水深73cmの低水路部,ついで2.5mの
1/5勾配の急斜面,さらに水深23cmで長さ40mの高水路部となっている.Fig.1に実験装置の概要を示す.
水路端の造波装置により孤立波を造波して実験を行った.高水路部の始点を基
準とし,高水路部にマングローブのモデルを設置し,その前後での波高,流速の計測
を行った.
Fig.2に計測地点及びモデルの概要を示す.波高,水平流
速は1m間隔でモデルの前後に1m計測を行った.水平流速は水深方向に5cm間隔で
計測をした.
モデルの位置はモデルの前面の位置が0,3,7,10m(入射波,砕波前,砕波,
砕波後)の4カ所で計測をした.マングローブは,根,幹,葉の3つの構造的な特徴
を持ち,それぞれに形状と投影面積による占有率を変えている.根,幹,葉のモデル
のそれぞれの占有率は2.74,0.75,31.65%である.また,根部の厚さは5cmである.
幹部は直径2cmで,20cm間隔の格子状に配置している.このモデルは波の伝播方向の
長さ(1m,2m),葉部の高さ(葉のモデルの底辺が水底から22cm,32cm)を変えることがで
き,葉部を取り外すこともできる(Table-1を参照).
Fig.1 実験装置概略
Fig.2 マングローブモデル
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.抵抗係数の算定
(1)運動方程式
実験で用いたマングローブモデルの影響を考慮するため,モデルの透過性, Manning抵抗則,付加質量を取り入れる.これらの係数を含む一次元の運動方程式は 次式の様になる1).
|
|
・・・・ ( 1 ) |
|
|
ここで,M:流量,D(=h+η):全水深,β:運動量補正係数,CM:付加質 量係数,Vobs:モデルの体積,V:モデルを含む水面下の全体積,n:粗度係数 を意味する.
(2)抵抗係数の算定方法
n,CMの各抵抗係数を(1)式をもとに実験デ
ータ(水位と流速)を入力することにより算定する.Mは水深方向に5cm間隔にとった
データを用いて算出した.
計算方法は運動方程式を差分化し,未知数の数だけ時間的に異なる運動方程式
をたてて行列を求め,逆行列を計算することにより算定をした.
(3)計算結果
Fig.3a-dに葉のモデルを高さ22cmに設定したマングロ
ーブのモデルをX=3〜5mに設置したとき(Case-3L2)の計算に用いた実験データと計
算結果のnと付加質量係数CMの時系列を示す.計算に用いた間隔は水
路方向にdx=2m,時間方向にdt=0.5sである.
摩擦力は流れに対して働くので,流れの小さな時(流れの向きが入れ替わる付
近や15秒以降)の値は無視することができる.また,Manningの粗度係数は等流を仮
定して用いられるものであるのでマングローブモデル内の流れが等流に近い区間
(12〜16秒)で安定した値が計算できる.実際このときの値は0.05程度になっている.
一方,付加質量係数は葉のモデルが水面よりも下にあるときのみ計算を行っている.
CMはばらついた値となっている.これは,実験の計測間隔が2mと非常に
長く設定したため,運動方程式を差分化する際に適切な空間間隔に設定できなかった
ためである.今後,この点をふまえた検討が必要がある.
Fig.4に葉のモデルを22cmに設定(Case-L)したマングロー
ブモデルをX=0〜2m(Case-0L2),
3〜5m(Case-3L2), 7〜9m(Case-7L2),
10〜12m(Case-10L2)に設置したときの計算されたマニングの粗度係数と体積占有
率との関係を示す.ここで,体積占有率はモデルの設置された区間における水面下の
全体積とマングローブモデルの体積との比を意味する.占有率が0.018付近のグルー
プは葉のモデルが水面からでているときのものである.多少ばらつきがあるものの,
nと占有率には正の相関があることがわかる.
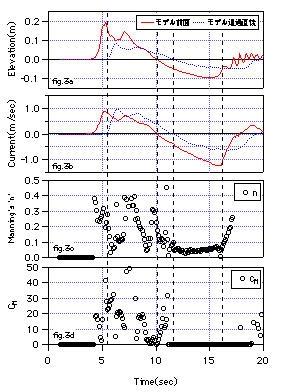
Fig.3a-d Calculation result of 'n' , 'CM'
Fig.4 Relation of 'n' and Volume Occupation Rate
5.終わりに
マニングの粗度係数と体積占有率との間に相関を見ることができた.今後検 討を重ね数式化を試みる.特に付加質量係数については今後さらに検討が必要であ る.
参考文献
1)榊山勉・阿部宣行・鹿島遼一(1990):ポーラスモデル による透過性構造物周辺の非線形波動解析,海岸工学講演会論文集,第 37巻,pp.554-558.